Generalized Autoencoder: A Neural Network Framework
for Dimensionality Reduction
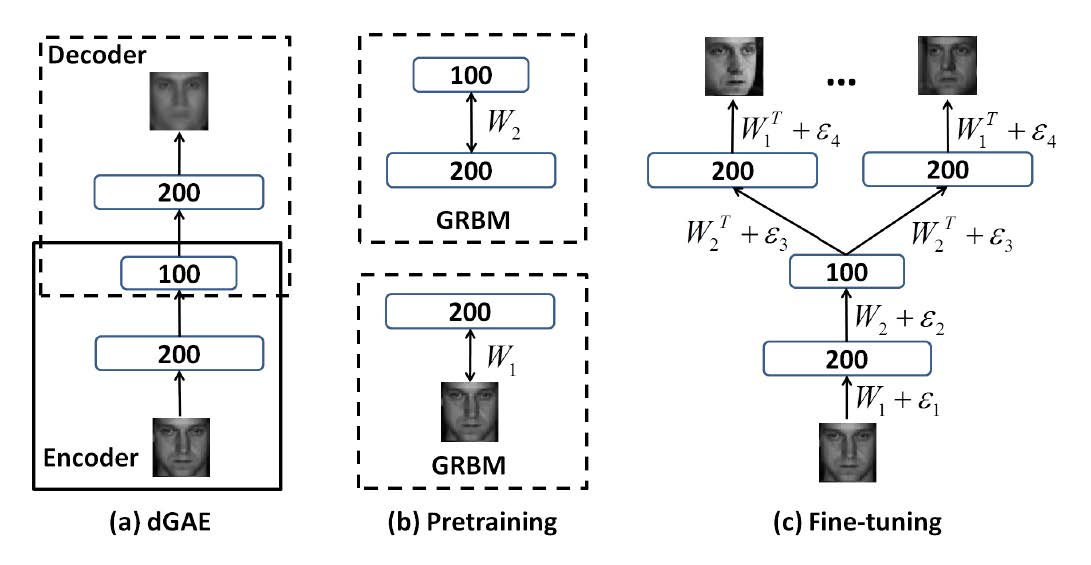 |
| Training a deep generalized autoencoder (dGAE) on the face dataset |
People
Wei Wang
Yan Huang
Yizhou Wang
Liang Wang
Overview
The autoencoder algorithm and its deep version as traditional dimensionality reduction methods have achieved great success via the powerful representability of neural networks. However, they just use each instance to reconstruct itself and ignore to explicitly model the data relation so as to discover the underlying effective manifold structure. In this paper, we propose a dimensionality reduction method by manifold learning, which iteratively explores data relation and use the relation to pursue the manifold structure. The method is realized by a so called "generalized autoencoder" (GAE), which extends the traditional autoencoder in two aspects: (1) each instance xi is used to reconstruct a set of instances {xj} rather than itself. (2) The reconstruction error of each instance (||xj-xi'||2) is weighted by a relational function of xi and xj defined on the learned manifold. Hence, the GAE captures the structure of the data space through minimizing the weighted distances between reconstructed instances and the original ones. The generalized autoencoder provides a general neural network framework for dimensionality reduction. In addition, we propose a multilayer architecture of the generalized autoencoder called deep generalized autoencoder to handle highly complex datasets. Finally, to evaluate the proposed methods, we perform extensive experiments on three datasets. The experiments demonstrate that the proposed methods achieve promising performance.
Paper
 |
Experimental Results
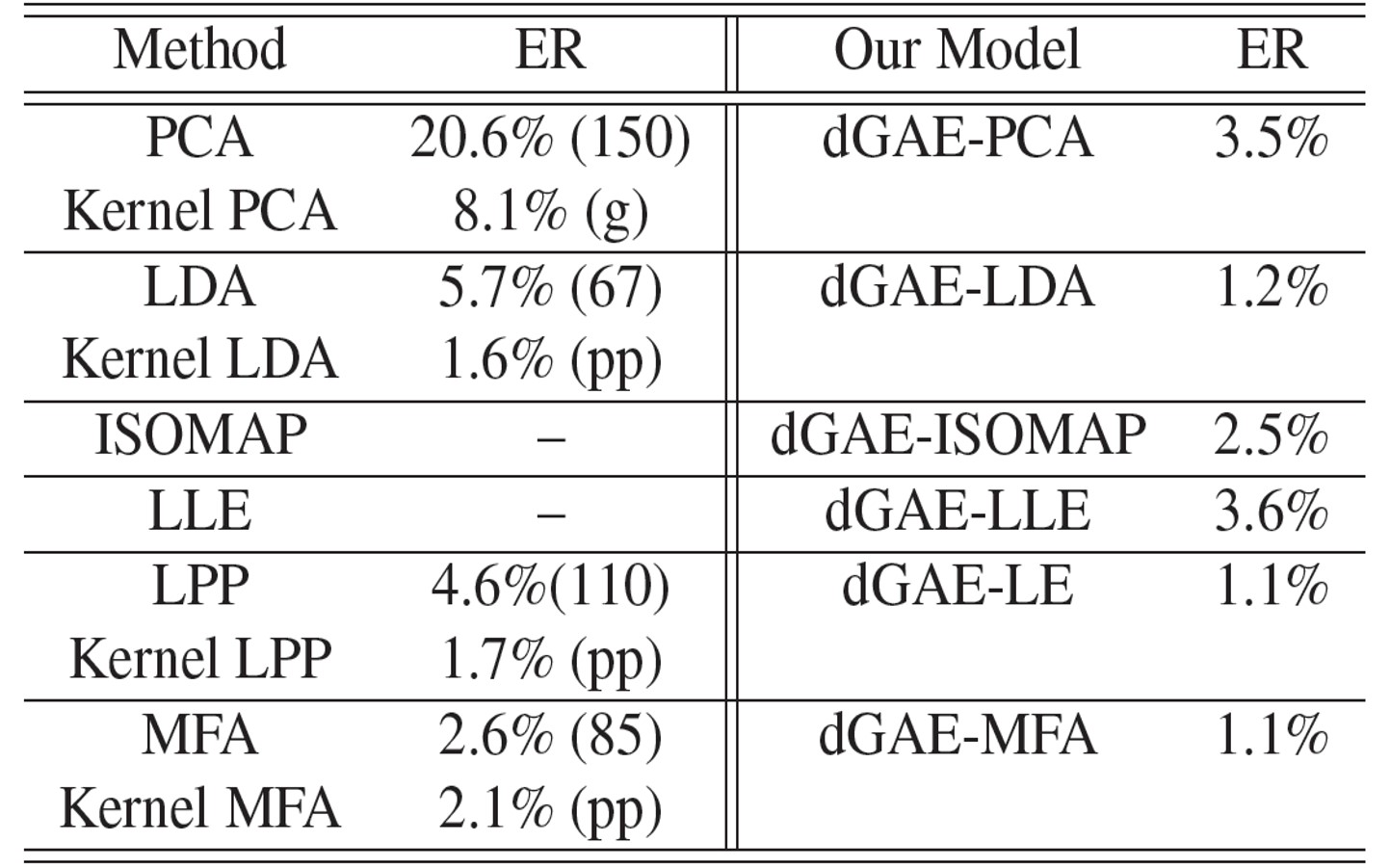
| Performance comparison on the CMU PIE dataset. ER is short for "error rate". The reduced dimensions are in parentheses. Our models use 100 dimensions. pp are short for "polyplus" kernels. | Performance comparison on the MNIST dataset. ER is short for "error rate". The reduced dimensions are in parentheses. Our models use 30 dimensions. pp is short for "polyplus" kernels. | |
 |
 |
Acknowledgments
This work is jointly supported by National Basic Research Program of China (2012CB316300), Hundred Talents Program of CAS, and National Natural Science Foundation of China (61202328).

